Cross Product (made easy - 2 simple ways)
A simple approach to compute a 3-dimensional vector cross-product
Computing the cross-product of two 3 dimensional vectors can be as easy as:
(1 - 2) + (3 - 4) + (5 - 6)
For each of the vector directions (I, J, K), the method is the same. You first go (down to the right) through the unit vector picking up 2 coefficients and return from below (up to the right) picking up the 2 coefficients to subtract:
Computing the coefficients in the [I] unit direction
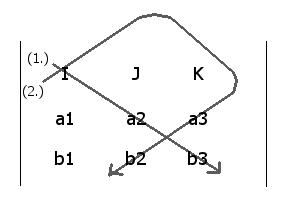
(1 - 2) = (a2b3 - a3b2) [I]
Computing the coefficients in the [J] unit direction
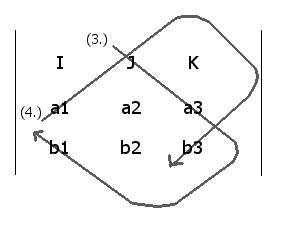
(3 - 4) = (a3b1 - a1b3) [J]
Computing the coefficients in the [K] unit direction
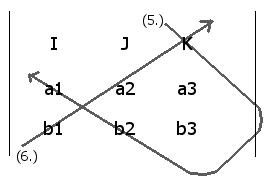
(5 - 6) = (b2a1 - b1a2) [K]
Final Solution (a x b)
a x b = (a2b3 - a3b2) [I] + (a3b1 - a1b3) [J] + (b2a1 - b1a2) [K]
Method Advantages
The beauty of the system is it allows the same sweeping motion through each of the unit vectors (first down to the right), then (back up to the right) picking up 2-coefficients each time. There is nothing you have to remember to do differently for (I) or (J) or (K).
I always found this approach much simpler to remember than trying to (ignore a single direction in a column vector and then trying to remember how (I) was different from (J) and then, again, how (K) was different from (I).
Here, just set up the matrix and simply do the same thing for each unit vector. Try it:
| I J K | | | | a1 a2 a3 | = a2b3-a3b2 [I] + a3b1-a1b3 [J] + b2a1-b1a2 [K] | | | b1 b2 b3 |
You Only Like Straight Lines? There is a Second Method
There are some that have a difficult time remembering how to go (down to the right) through the unit vector picking up 2 coefficients and return from below (up to the right) picking up the 2 coefficients to subtract. Luckily there is a second method that involves only straight lines.
The method requires that you duplicate the (I, J) column vectors just to the right of the (K) column. After doing so, your method for computing the cross product simply requires you go (down to the right) through the unit vector picking up 2 coefficients and return from below (up to the right) through the appended (I, J) unit vectors picking up the 2 coefficients to subtract. (note: you use the same (K)
Computing the coefficients in the [I] unit direction
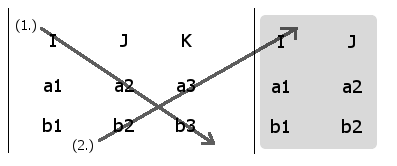
(1 - 2) = (a2b3 - b2a3) [I]
Computing the coefficients in the [J] unit direction
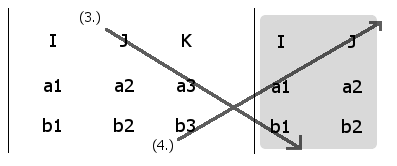
(3 - 4) = (a3b1 - b3a1) [J]
Computing the coefficients in the [K] unit direction
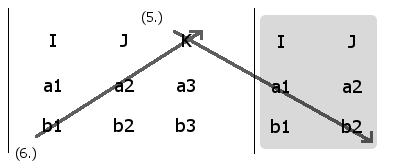
(5 - 6) = (a1b2 - b1a2) [K]
Final Solution (a x b)
a x b = (a2b3 - b2a3) [I] + (a3b1 - b3a1) [J] + (a1b2 - b1a2) [K]
(note: only the order of multiplication has changed -- nothing else)
Courtesy of an old Attorney and Aerospace Engineer from Texas A&M




